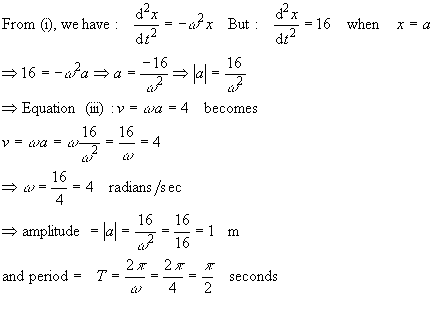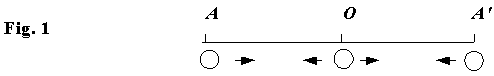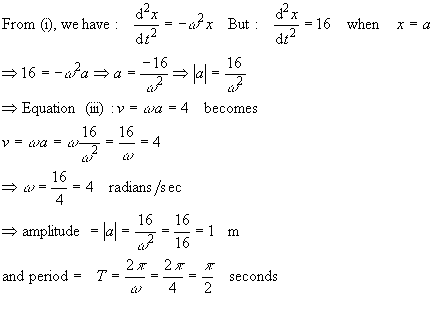A particle moving with simple harmonic motion moves along a path with an acceleration which is:
Simple harmonic motion occurs in many mechanics problems eg those involving springs, elastic strings, pendulums, vibrating planes, etc.
A particle of mass is performing simple harmonic motion with a maximum velocity of 4 m/s and maximum acceleration of 16 m/s2. Find the amplitude and period of the motion.
The physical model in Fig. 1 shows the particle at the mid-point O, and at each end of its path, A and A?. Fig. 2 shows a table of the characteristics of the motion of the mass when at points A, O, A?
| Characteristic |
At A |
At O |
At A? |
| Velocity |
0 |
Maximum |
0 |
| Direction of motion |
Towards O |
Either direction |
Towards O |
| Acceleration |
Maximum |
0 |
Maximum |
| Direction in which acceleration is acting |
Towards O |
Does not apply |
Towards O |
Mathematical equations are constructed involving relationships between mass, time, distance, velocity and acceleration:
From the standard simple harmonic motion equations:
(i)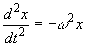 
where w is a constant and x is the displacement from O
(ii)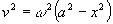 
where a = amplitude = OA = OA?lt;/P>
(iii) T =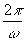 
Given:
Maximum velocity = 4 m/s. This occurs when distance of the particle from the equilibrium point is 0 (i.e. when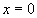 
and acceleration =
)
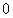Equation (ii) becomes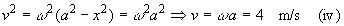 
The maximum acceleration is 16 m/s2. This occurs when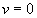 
, i.e. when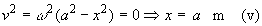 
x is a maximum Þ x = amplitude = a
