A body of mass m moving with velocity v has a kinetic energy of ![]() mv2. A body of mass m rotating about a fixed axis with angular velocity w will have a “rotational” kinetic energy of
mv2. A body of mass m rotating about a fixed axis with angular velocity w will have a “rotational” kinetic energy of ![]() Iw2 where I = Moment of Inertia of the body
Iw2 where I = Moment of Inertia of the body
Rotation of a Rigid Body
Sample Problem
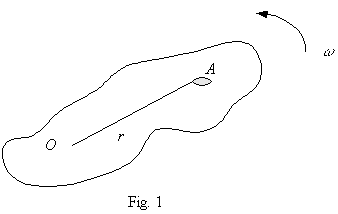
A rigid body is rotating with angular velocity w about an axis through a point O which is perpendicular to the plane of the body (See Fig. 1). Derive an expression for the kinetic energy of the body in terms of w and the Moment of Inertia, I
Solution
Fig. 1 illustrates the physical model in the problem:
Consider a particle of the rotating body of mass m at A (assume |OA| = perpendicular distance from A to the axis through O = r) travelling at speed v. (See Fig. 1) Its kinetic energy = ![]() mv2.
mv2.
The next step is to identify the energy in the system. Then a mathematical model can be constructed:
See the “Circular Motion” example: this shows that the velocity of this particle is v = rw so that its kinetic energy can be expressed as ![]() m(rw)2 =
m(rw)2 = ![]() mr2w2
mr2w2
To find the kinetic energy of the whole body we sum the kinetic energies of all the individual particles which make up the body. Therefore: total kinetic = S ![]() mr2w2. As w is the same for each individual particle, the total kinetic energy can be expressed as
mr2w2. As w is the same for each individual particle, the total kinetic energy can be expressed as ![]() w2S mr2. The quantity S mr2 is called the Moment of Inertia and is usually denoted by the letter I.
w2S mr2. The quantity S mr2 is called the Moment of Inertia and is usually denoted by the letter I.