The Section on Velocity and Acceleration deals with the linear motion of bodies and the interrelationships of the main variables, time, distance, velocity and acceleration. For simplicity it is assumed that the dimensions and masses of the bodies can be ignored i.e. they are treated as particles or points.
Velocity and Acceleration
Sample problem: Ball projected vertically upwards
A ball is projected vertically upwards with a velocity of 19.62 m/s (See Fig. 1).
Find:
(a) The time taken for the ball to reach the greatest height.
(b) The greatest height reached.
(c) The position of the ball after t = 4 and t = 6 seconds.
(d) The time taken to reach a height of 9.81 m above the point of projection
(assume g = 9.81 m/s2).
Solution
Fig. 2 outlines the problem in more detail:
Stage 1 AB: Ball is rising to its greatest height
Stage 2 BC: Ball is falling under gravity from its greatest height
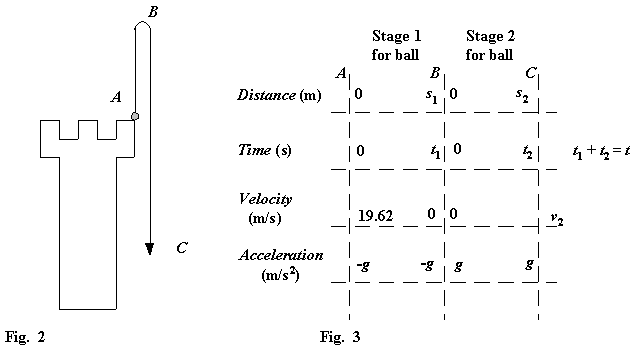
Fig. 3 shows information regarding distance, time, velocity and acceleration at the start and finish of each Stage which can be used to construct mathematical equations to simulate the physical model.
Use general equations for linear motion: (i) ![]() (ii)
(ii) ![]()
(a) The time taken for the ball to reach the greatest height
When the ball reaches its greatest height (at B) it has a speed v = 0.
Thus, from equation (ii):
Time taken to reach greatest height is t where: 0 = 19.62 ?gt Þ t = 2 seconds
(b) The greatest height reached
Let the maximum height be h. Using equation (i) when s = h and t = 2 seconds gives: ![]()
(c) The position of the ball after t = 4 and t = 6 seconds
The ball reaches the maximum height (at B, 19.62 m above A) in 2 seconds.
From Fig. 3: Total time of motion of the ball = t = t1 + t2
Since t = 4 seconds (given) and t1 = 2 seconds Þ t2 = 2 seconds
In other words, when t = 4 seconds the ball has reached its highest point and has been falling from this point for 2 seconds. The distance travelled by the ball (which falls from rest) in 2 seconds is s where:
s = ![]() = 19.62 m
= 19.62 m
Thus, after 4 seconds the ball is 19.62 ?19.62 = 0 m below the point of projection (i.e. at same level as A).
When t = 6 seconds the ball has reached its highest point and has been falling from this point for 4 seconds (i.e. t2 = 4 seconds). The distance travelled by the ball (which falls from rest) in 4 seconds is s where
s = ![]() = 78.48 m
= 78.48 m
Thus after 4 seconds the ball is 19.62 ?78.48 = 58.86 m below the point of projection.
(d) The time taken to reach a height of 9.81 metres above the point of projection
Using equation (i) we have: ![]()
If s = 9.81 m and u = 19.62 m/s then
9.81 = 19.62 t – ![]() g t2
g t2
Þ ![]() g t2 ?19.62 t + 9.81 = 0
g t2 ?19.62 t + 9.81 = 0
Þ t2 ?4 t + 2 = 0
Solving this equation gives t = 2 ?Ö 2 seconds. Thus the ball reaches a height of 9.81 m after 2 – Ö 2 seconds of flight while ascending and again after 2 + Ö 2 seconds of flight while descending.