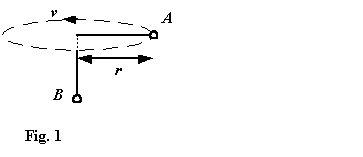
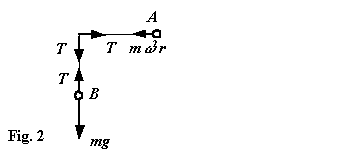Menu

Circular motion

Circular Motion problems deal with particles moving in horizontal circles with uniform speed and particles moving in vertical circles under gravity.

A body moving at a constant speed in a straight line will continue to move in a straight line in the absence of other forces. If a force, acting in the same direction, is applied to the body, the body will accelerate. If a force, acting in the reverse direction, is applied, the body will decelerate. In other words, forces acting parallel to the line of motion can only change the speed of the body.

In the case of circular motion, a force, acting in a direction perpendicular to that of the body, is applied to the body. The body will change direction and travel in a circle but it will continue to move at the same speed.

Problem
Solution

Sample problem: Motion in a horizontal circle

Two particles, A and B, each of mass m are connected by a string which passes through a hole in a smooth table. One particle rotates in a horizontal circle on the table, the other remains suspended underneath the table (See Fig. 1). If the suspended particle is to remain at rest, how many revolutions per minute does the particle on the table have to perform in a radius of (a) r = 0.1 metres, (b) r = 0.5 metres ?

The physical model of the problem is described with the aid of a diagram in Fig. 1:

Solution

Fig. 2 show the forces acting in the physical model to help us construct the mathematical equations:

The forces acting in the system are shown in Fig. 2:

T = Tension in the string in Newtons

w = Angular velocity of rotating particle in radians/second

For particle A: T = mw 2r N

For particle B: T = mg N

These mathematical equations describe how the physical model will behave.

Therefore: mg = mw 2r for no movement of particle B to occur.

Þ g = w 2r Þ w 2 = Þ w =

 

As: 1 revolution = 360o = 2p radians

Þ 1 revolution/second = 2p radians/second

Þ w = 2p f (where f = frequency in revolutions/second)

Þ f

(a) r = 0.1 m Þ f = 1.576 revolutions/second = 94.58 revolutions/minute.

(b) r = 0.5 m Þ f = 0.705 revolutions/second = 42.298 revolutions/minute.

Copyright 2016 Mechanics Made Easy a question and answer book